07-运筹学-状态转移矩阵

状态转移矩阵 transition matrix

    Example. In a certain city, if today is sunny, tomorrow will be sunny 80% of the time. If today is cloudy, tomorrow will be cloudy

60% of the time. Supposing today is sunny, what is the probability it will be cloudy the day after tomorrow

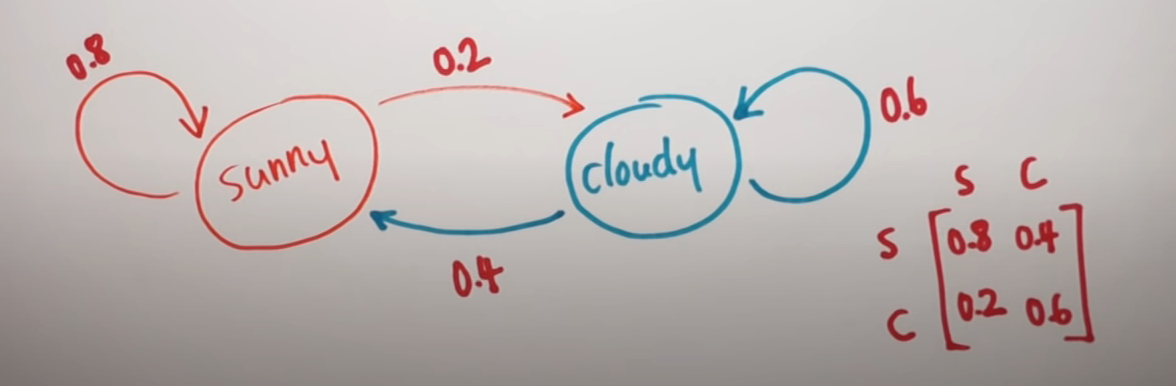
tomorrow:

    today is sunny， then : sunny 80%, cloudy 20%

after tomorrow:

    then： cloudy is  80% * 20% + 20% * 60% = 28%

So today is sunny, 28% it will be cloudy the day after tomorrow

来两个中文的例子

例1

假设市场上某种商品有两种品牌A和B，当前的市场占有率各为50%。根据历史经验估计，这种商品当月与下月市场占有率的变化可用转移矩阵P来描述：

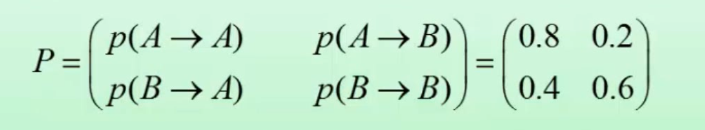
其中  p(a->b) 是A的市场占有份额中转移给B的概率，依次类推。这样，两个月后的这种商品的市场占有率变化为_。

    A.A的份额增加了10%，B的份额减少了10%

    B.A的份额减少了10%，B的份额增加了10%

    C.A的份额增加了14%，B的份额减少了14%

    D.A的份额减少了14%，B的份额增加了14%

解析：

    1. 1个月后

    A的市场占有率为： 50% * 80% + 50% * 40% = 60%

    B的市场占有率为： 50% * 20% + 50% * 60% = 40%

    2. 2个月后

    A的市场占有率为： 60% * 80% + 40% * 40% = 64%

    B的市场占有率为： 60% * 20% + 40% * 60% = 36%

因此A的市场份额增加了14%， B的市场份额减少了14%， 答案就是C了。

例2

    某类产品n种品牌在某地区的市场占有率常用概率向量u=（u1，u2，…，un）表示（各分量分别表示各品牌的市场占有率，值非负，且总和为1）。市场占有率每隔一定时间的变化常用转移矩阵Pn*n表示。设初始时刻的市场占有率为向量u，则下一时刻的市场占有率就是uP，再下一时刻的市场占有率就是uP2，…。如果在相当长时期内，该转移矩阵的元素均是常数，则市场占有率会逐步稳定到某个概率向量z，即岀现zP=z。这种稳定的市场占有率体现了转移矩阵的特征，与初始时刻的市场占有率无关。

    假设占领某地区市场的冰箱品牌A与B，每月市场占有率的变化可用如下常数转移矩阵来描述，则冰箱品牌A与B在该地区最终将逐步稳定到市场占有率为多少？

解析：

    状态转移矩阵的特点：

    最终结果稳定，这种稳定的状态体现了转移矩阵的特征，与初始时刻的状态无关。、

    假设最终A稳定在n，B稳定在m。

    那么有：

    ① 0.8n + 0.4m = n

    ② 0.2n + 0.6m = m， 由 ①②得到 n = 2m

    因为m + n = 100% 也就是1

    最终稳定状态时， A为 2/3 B为1/3