04-线性规划

题目描述： 

在如下线性约束条件下：2x+3y≤30；x+2y≥10；x≥y；x≥5；y≥0，目标函数2x+3y的极小值为（）。

题目分析：

这是2018年系统架构设计师软考的真题，刚读完题，感觉毫无头绪吧？ 这么多条件。

这类型的题，是典型的线性规划问题，简单粗暴点，可以这样求解：

    1. 使用两两条件结合，求得x、y的值；

    2. 看其他条件是否满足

    2.1 如果满足，然后求2x+3y的值是多少， 记录下这个值记作 min_n（n为1、2、3、4...），然后回到1

    2.2 如果不满足，回到1

    3. 从 min_n 中选最小值

这样解题的话，很容易漏掉两两组合的问题，同时验证的时候，也很可能漏掉某个条件。

我们可以画图解决：

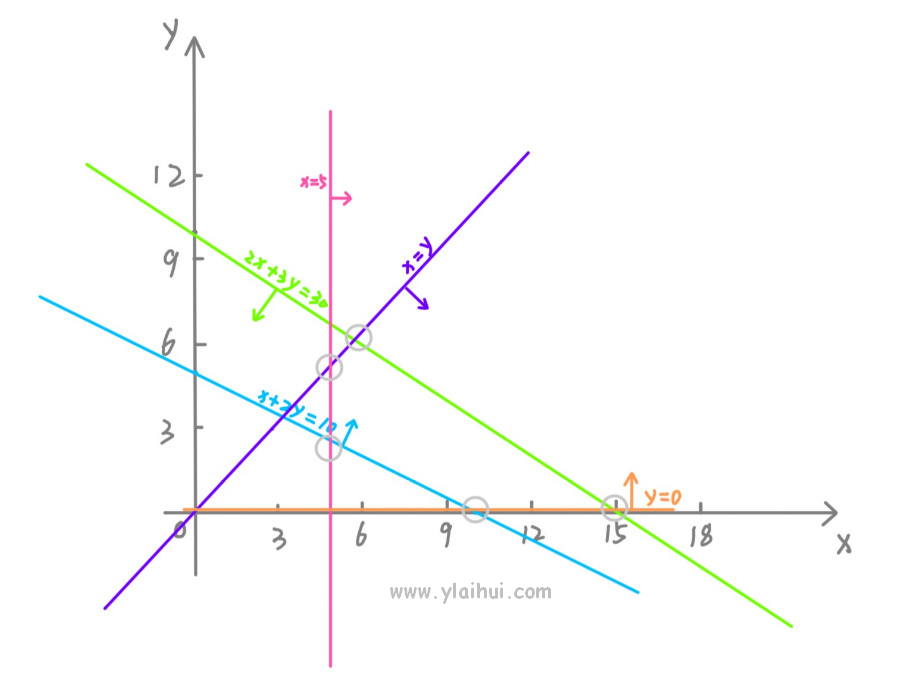
所有的条件等于时，将函数的坐标图画出来，条件为“不等”的区域就是每条直线上的方向指示的区域。

我们发现，所有的条件都满足，会围成一个多边形，也就是图中五个灰色的圆圈围成的区域。

因为是需要求2x+3y 的极值问题，对于 2x+3y<=N，是一条直线，极小值应该在上图中某个圆圈的位置。

粗暴点，可以将上面的5个交点 (12,18), (5,5), (5,5/2), (10,0), (15,0),的坐标一个个带入 2x+3y 求值。

最终 2x+3y  在 (5,5/2)点上值最小，最小值为 17.5