02-最短路径

题目描述:

有一批货物要从城市s发送到城市t，线条上的数字代表通过这条路的费用（单位为万元）。那么，运送这批货物，至少需要花费多少万元？

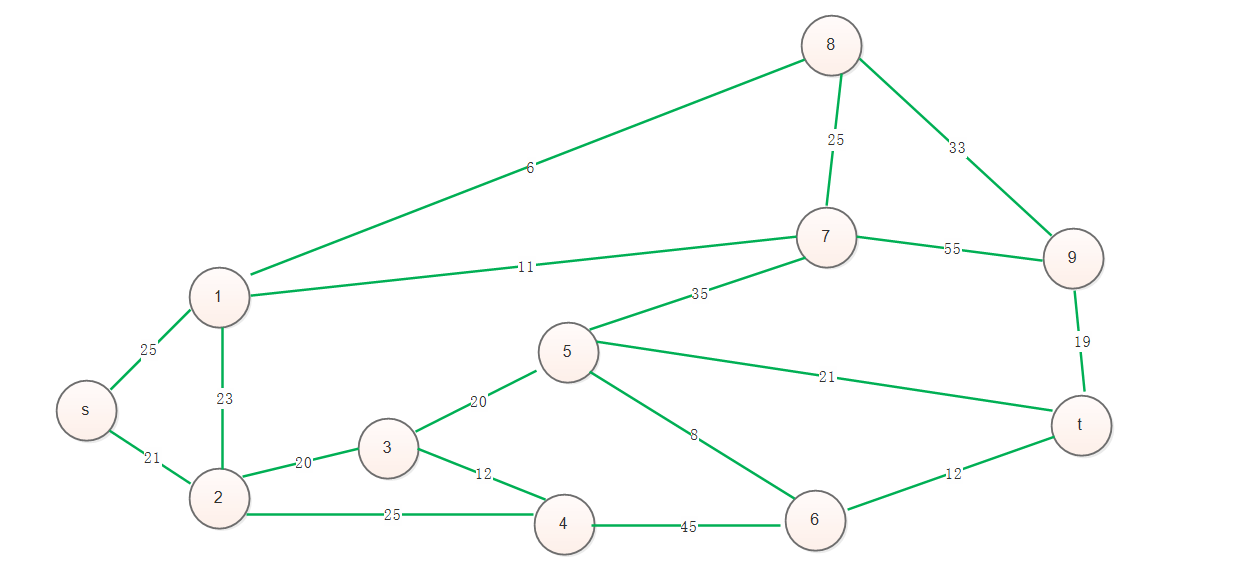
解析：

    我们做项目的时候，经常会用到"时标网络图"、"双代号网络图"吧？ 不过双代号网络图的边是由方向的，也就是任务是由前后依赖关系的，根据每个活动的依赖关系和活动预估的历时，我们可以得到项目的工期，关键路径等等。

    本题与项目管理中用到的“双代号网络图”类似，但是有区别的是，本题的图中边是没有方向的，是一个图，应该是无向有权图。

    题目要我们算出s到t花费的费用最少，也就是路径上的各个边加起来的和最小，找到这个路径，并计算这个最小值是多少。

    本题我们可以使用“动态规划的思维”，要想从s到t“值”最小，我们可以通过5/6/9的最小计算得到。

    假设5/6/9的最小分别为 f(5) f(6) f(9)，那么求得到t的最小就是 min(f(5) + 21, f(6) + 12, f(9) + 19 )，5/6/9的最小有需要借助他们各自的节点推导得到。这就是动态规划的递推思维。

根据以上分析，我们在图上依次正向递推：

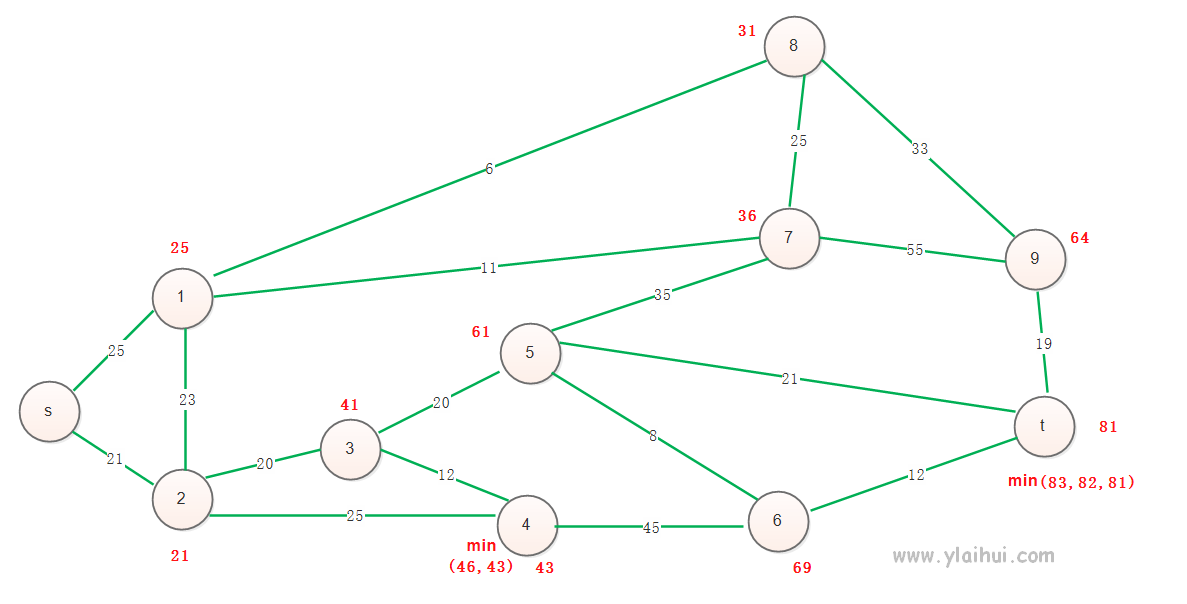
到1的最小为 min(25, 21+23),也就是25

到2的最小为min(21, 25+23)，也就是21

到3的最小为min(21+20, 21+25+12),其他的路径就不需要看了，肯定比这两个大。

依次类推...

最终求得s到t的最小值为 81。 这就是动态规划的算法逻辑，求解最短路径问题。