07-概念模型设计-规范化理论

规范化理论的价值与用途

    非规范化的关系模式，可能存在的问题： 数据冗余、更新异常、插入异常、删除异常

    规范化理论的价值也用途就是解决以上的问题。

    并非规范化程度越高越好，设计的时候，尽可能高，但是不要过分设计。 一项指标提的很高，另一项指标就下降了，比如规范化程度越高，那么多个表需要连接查询，那么查询性能就降低了。

求候选关键字

求候选码

    1. 首先应该找出F中所有的决定因素， 即找出出现在函数依赖规则中“->”左边的所有属性， 组成集合U1

    2. 在从U1中找出一个属性或属性组K，运用推理公式系统及理论， 使得K->U， 而K真子集K' -> U不成立

    3. 这样就得到了关系模式R的一个候选码， 找遍U1属性的所有组合， 重复过程2， 最终得到关系R的所有候选码

    如果已经找到了一个候选码K，K是U1的一个子集，那么找下一个候选码时， 就不需要考虑K与U1中其他属性的组合。 

图解法

    1. 首先将函数依赖关系，用“有向图”的形式表示

    2. 入度为0的属性，并以该属性集合为起点，尝试遍历整个有向图， 若能正常遍历图中的所有节点， 则该属性集即为关系模式的候选键。

    3. 若入度为0的属性集不能遍历图中的所有节点， 则需要尝试性的将一些中间节点（既有入度也有出度的节点）并入入度为0的属性集中，直至该集合能遍历所有结点， 集合为候选键。

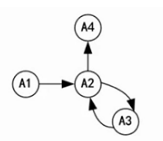
候选码：A 

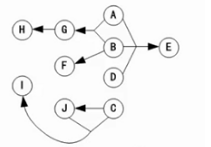
候选码：ABCD

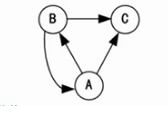
候选码：B

范式

    规范化越高，往往带来性能问题，所以一般采用比较折中的办法解决规范化问题，3NF左右就差不多。

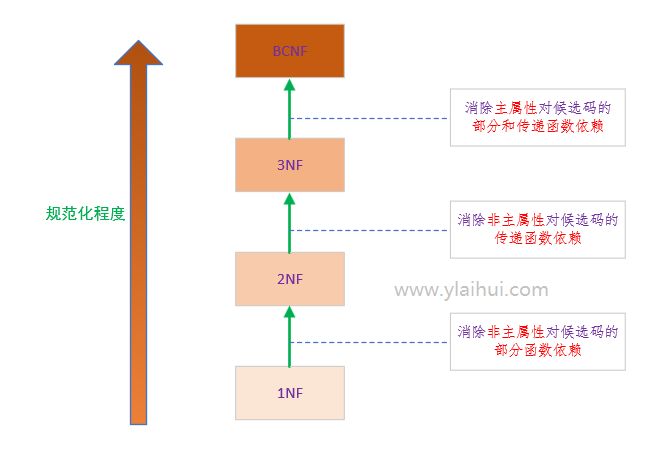
第一范式

    1NF， 在关系模式R中， 当且仅当所有域只包含原子值，即每个分量都是不可再分的数据项， 关系R是第一范式。

第二范式

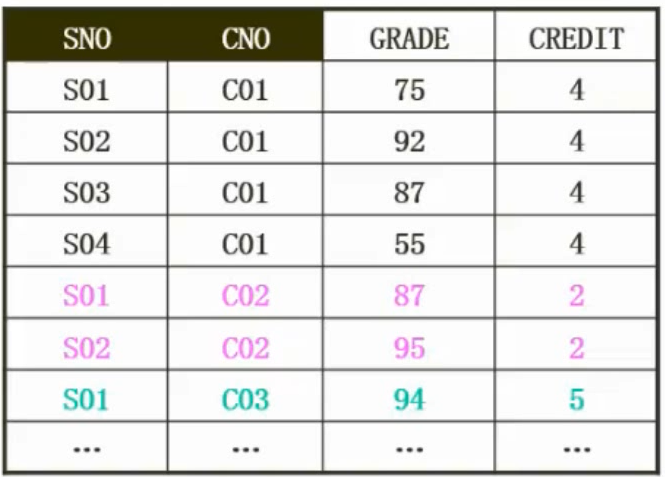
    2NF 当且仅当 R是1NF， 并且每个非主属性完全依赖于主键（不存在部分函数依赖）时， 关系R为第二范式。 存在非主属性部分函数依赖于码

    例：

    学号， 课程号 -> 成绩

    课程号 -> 学分 （每门课程学分是固定的）

    存在数据冗余： SNO 为 S01/S02/S03/S04 并且 CNO为 C01 时， 记录了4个4， 也就是C01的学分为4， 存在数据冗余

    更新异常（如：更新课程的学分，可能更新不全，只更新第一条， 后面三条没更新导致数据不一致）

    删除异常（删除学生的成绩， 会将课程所对应的学分信息删除）

    插入异常（新开某个课程，现在没学生选这个课程， 是无法录入表中的）

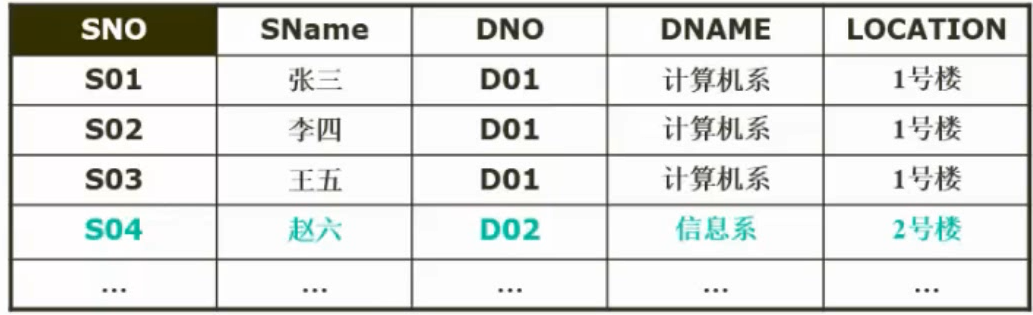
第三范式

    3NF， 当且仅当R是2NF， 不存在非主属性传递依赖于码时， 关系R是第三范式。

    例：

    主属性只有一个， 显然符合2NF的要求。 肯定不存在部分函数依赖于码的

    但是存在 DNO -> DNAME 、 DNO -> LOCATION ，同样存在 数据冗余、插入、删除、更新异常， 存在非主属性传递依赖于码

BC范式

    R是关系模式， F是依赖集，当且仅当F中每个依赖的决定因素必定包含R的某个候选码时， R属于BCNF。

    所有的函数依赖写出来， 函数依赖的左边必须都是候选键。

    R的F包含：  SJ->T  T->J, 其候选码为： SJ 和 ST， 对于函数依赖 T->J， T不是候选键，所以R不是BCNF。

模式分解

    一个关系分解为多个关系，分解后的关系不存在包含关系。分解后的函数依赖属于F的闭包

模式分解的三种情况

    分解具有无损连接性（分解后可以再连接，数据不会丢失和多余）

    分解保持函数依赖（分解后的函数依赖集跟未分解的函数依赖集等价）

    分解既要无损连接性，又要保持函数依赖

    无损连接和函数依赖是两个独立的标准， 无损不一定是保持函数依赖，反之亦然。

模式分解例子

    关系模式Std( Sno, Sdept, Mname )，其属性组上的函数依赖集是：

        F= { Sno->Sdept, Sdept -> Mname }

    由前面介绍的规范化可知， Std∈2NF, 而 Std不属于3NF， 所以该关系模式存在插入异常、删除异常、数据冗余和更新异常。 因此， 需要分解该关系模式， 使其成为更高级范式的关系模式。 对关系模式Std分解至少有如下几种方案。

    模式分解的几个例子：

        R11( Sno, Mname )  和 R12(Sdept, Mname )    ---无法拼合， 分解无意义

        R21( Sno, Sdept )  和 R22(Sno, Mname )   ---  

        R31( Sno, Sdept ) 和  R22(Sdept , Mname )

        R41( Sno ) 和  R42(Sdept  ) 和 R43( Mname )

    因为把低级关系模式分解为若干个高级关系模式的方法并不唯一，所以只有哪些能够保证分解后关系模式与原关系模式等价的方案才有意义。 常用的等价标准： 要求分解处理具有无损连接性和保持函数依赖性。

无损连接

    将某个关系R分解为多个子关系后， 各个子关系的投影的自然连接与原来关系R等价（简言之： 分解后的多个关系模式可以还原为原来的关系模式，那么就是无损分解）

    判断无损连接的定理，只要两个定理满足其中一个就可判断是否满足无损连接（是否满足交集决定差集）

    无损连接例子：

保持函数依赖

    关系模式Std( Sno, Sdept, Mname )，其属性组上的函数依赖集是：

        F= { Sno->Sdept, Sdept -> Mname }

    分解为 R1（Sno, Mname） 和R2( Sdetp, Mname )

    分解方案： F1 U F2  = { Sno -> Mname, Sdept->Mname }

            分解的R1和R2不是保持函数依赖

    分解为 R3（Sno, Sdetp） 和R4( Sdetp, Mname )

    分解方案： F3 U F4  = { Sno -> Sdetp , Sdept->Mname }

        显然被F逻辑蕴含的函数依赖，也被 F1∪F2逻辑蕴含

分解具有无损连接性和分解具有保持函数依赖， 这是两个独立的标准：

    具有无损连接性的分解不一定保持函数依赖

    保持函数依赖的分解也不一定具有无损连接性