Hash表
哈希表介绍
2021-06-01 587 2
简介
1. 散列的实现
我们都知道数组支持按照下标随机访问数据,散列表在实现的时候借助了这一点。
散列表其实就是数组的一种扩展,由数组演化而来。
给定一个数组 [11, 15, 16, 18, 19], 如果想要查找18这个数据, 那么我们只能通过暴力求解的方法,依次遍历整个数组,查找18。
如果我们提前知道了数据18的下标, 也就是18 在数组[11, 15, 16, 18, 19] 中的下标是 3, 那么我们可以在O(1)的时间复杂度找到18这个数据。
对于任意一个数据,如何得到下标呢? 这就是接下来要讲的哈希函数的作用。
哈希函数就是对数据计算了一个特征值,这个特征值就是数据在数组中的下标,为了方便说明哈希表和哈希函数, 我们将上面介绍的数组改为字符串数组。
["0X99811", "0XFF815", "0X00116", "0X44518", "0X44619"]
通过分析,我们发现这些字符串数据存在一定的规律, 字符串后两位都是1X,为了能快速的在数组中找到字符串“0X44518”,我们让该数据在数组中的下标为8, 那么通过arr[8] 就可以直接获取数据“0X44518”了。
也就是 index = f(0X44518) = 8,简单起见,我们可以让f()的功能为 除以10,取余数。(这里取模运算,知识为了简单起见,实际应用中,hash函数的设计,需要考虑数据特征、简单、高效等问题)
那么 0X44518 % 10 = 8
这里的f()就是哈希函数
数值 0X44518 是key
对象 “0X44518” 是value
经过hash之后,原来的字符串数组就变为:
[null, "0X99811", null, null, null, "0XFF815", "0X00116", null, "0X44518", "0X44619"]
通过哈希函数, f(0X44518) 也就是 0X44518 %10 = 8, 那么字符串"0X44518"在数组中的下标为 8, 通过arr[8] 就可以直接获取该字符串对象
获取数据或者查找数据的算法时间复杂度都为O(1),虽然数组中增加了null,增加了数组占用的内存,但是这是一种空间换取时间的思想。
2 如何设计哈希函数
1. 哈希函数计算得到的哈希值是一个非负整数,这个要求是必须的, 因为数组的下标没有负数。
2. 如果 key1 = key2,那 hash(key1) == hash(key2), 也就是对于同一个key, 得到数组的下标是相同的。
3. 如果 key1 ≠ key2,那 hash(key1) ≠ hash(key2), 这个要尽量满足,如果不同的key产生了相同的hash值,比如 0X44518 和 0X44528 那么arr[8] 位置就需要保存两个字符串, "0X44518" 和 "0X44528",对于数组这是不允许的,这就是hash冲突。如何解决hash冲突,后面会讲到。
散列函数的设计不能太复杂。过于复杂的散列函数,势必会消耗很多计算时间,也就间接地影响到散列表的性能。其次,散列函数生成的值要尽可能随机并且均匀分布,这样才能避免或者最小化散列冲突,而且即便出现冲突,散列到每个槽里的数据也会比较平均,不会出现某个槽内数据特别多的情况。
数据分析法
分析需要进行hash计算的key的特征,比如长度特点和分布
例如:身份证后8位, 手机号后5位等的,就会使得hash后的数据比较均衡分布
如果选用身份证号的前6位,那么会出现大量从冲突,手机号前4位也是一样的。
3. 解决hash冲突
3.1 开放寻址法
开放寻址法的核心思想是,如果出现了散列冲突,我们就重新探测一个空闲位置,将其插入。那如何重新探测新的位置呢?一个比较简单的探测方法,线性探测(Linear Probing)。当我们往散列表中插入数据时,如果某个数据经过散列函数散列之后,存储位置已经被占用了,我们就从当前位置开始,依次往后查找,看是否有空闲位置,直到找到为止。
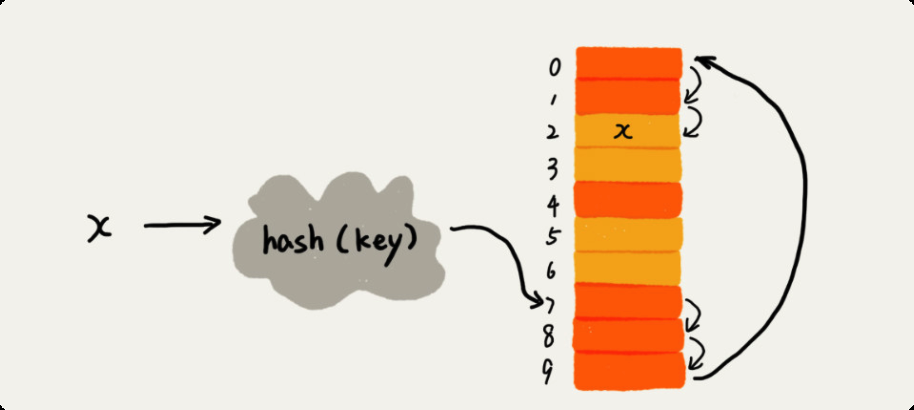
从图中可以看出,散列表的大小为 10,在元素 x 插入散列表之前,已经 6 个元素插入到散列表中。x 经过 Hash 算法之后,被散列到位置下标为 7 的位置,但是这个位置已经有数据了,所以就产生了冲突。于是我们就顺序地往后一个一个找,看有没有空闲的位置,遍历到尾部都没有找到空闲的位置,于是我们再从表头开始找,直到找到空闲位置 2,于是将其插入到这个位置。
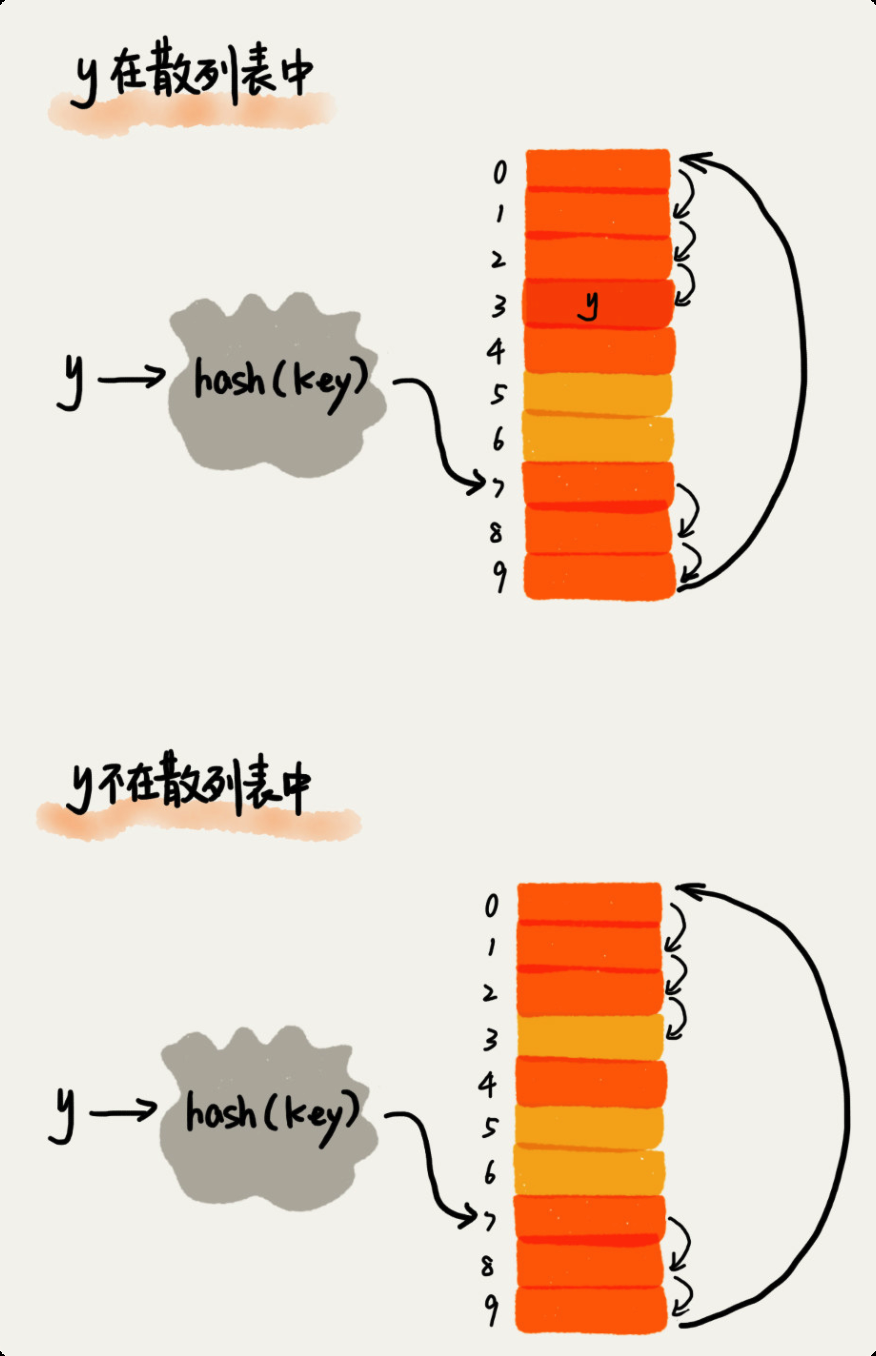
在散列表中查找元素的过程有点儿类似插入过程。我们通过散列函数求出要查找元素的键值对应的散列值,然后比较数组中下标为散列值的元素和要查找的元素。如果相等,则说明就是我们要找的元素;否则就顺序往后依次查找。如果遍历到数组中的空闲位置,还没有找到,就说明要查找的元素并没有在散列表中。
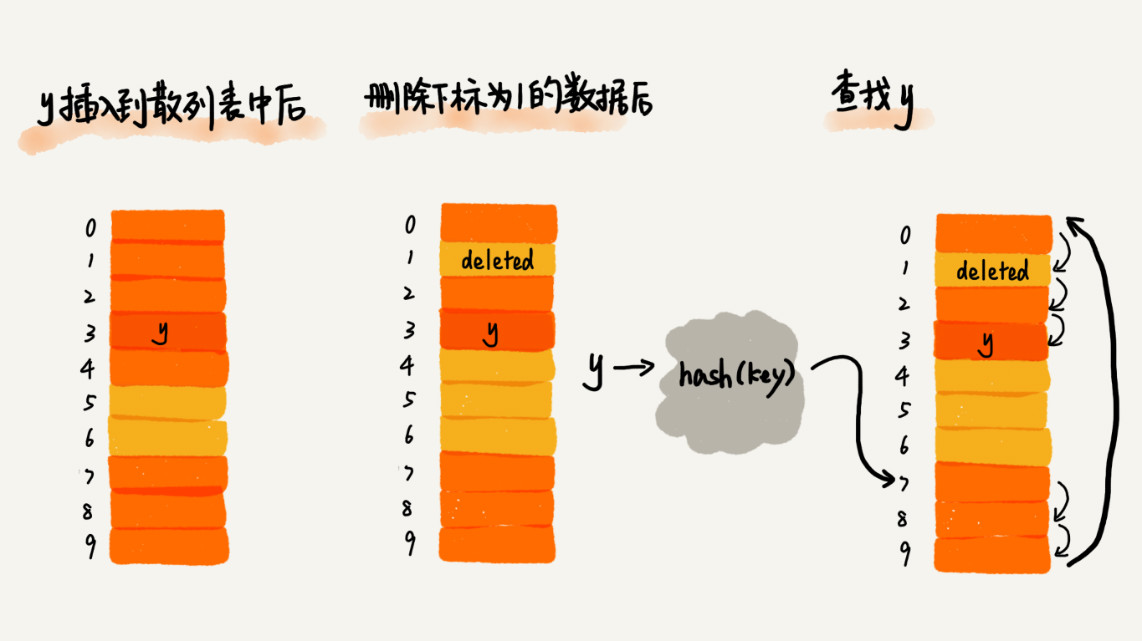
散列表跟数组一样,不仅支持插入、查找操作,还支持删除操作。对于使用线性探测法解决冲突的散列表,删除操作稍微有些特别。我们不能单纯地把要删除的元素设置为空。
这是为什么呢?还记得我们刚讲的查找操作吗?在查找的时候,一旦我们通过线性探测方法,找到一个空闲位置,我们就可以认定散列表中不存在这个数据。但是,如果这个空闲位置是我们后来删除的,就会导致原来的查找算法失效。本来存在的数据,会被认定为不存在。这个问题如何解决呢?我们可以将删除的元素,特殊标记为 deleted。当线性探测查找的时候,遇到标记为 deleted 的空间,并不是停下来,而是继续往下探测。
3.2 链表法
可以将字符串数组改为链表数组, 数组中的每一个元素是一个链表, 发生hash冲突时,arr[i] 位置可以保存多个字符串。使用链表是解决hash冲突的一种办法,还可以使用红黑树解决hash冲突。hash冲突时不可避免的, 业界著名的MD5、SHA、CRC等哈希算法,也无法完全避免这种hash冲突。而且,因为数组的存储空间有限,也会加大散列冲突的概率。所以我们几乎无法找到一个完美的无冲突的散列函数,即便能找到,付出的时间成本、计算成本也是很大的,所以针对散列冲突问题,我们需要通过链表或树来解决。
链表法是一种更加常用的散列冲突解决办法,看下图,在散列表中,每个“桶(bucket)”或者“槽(slot)”会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。
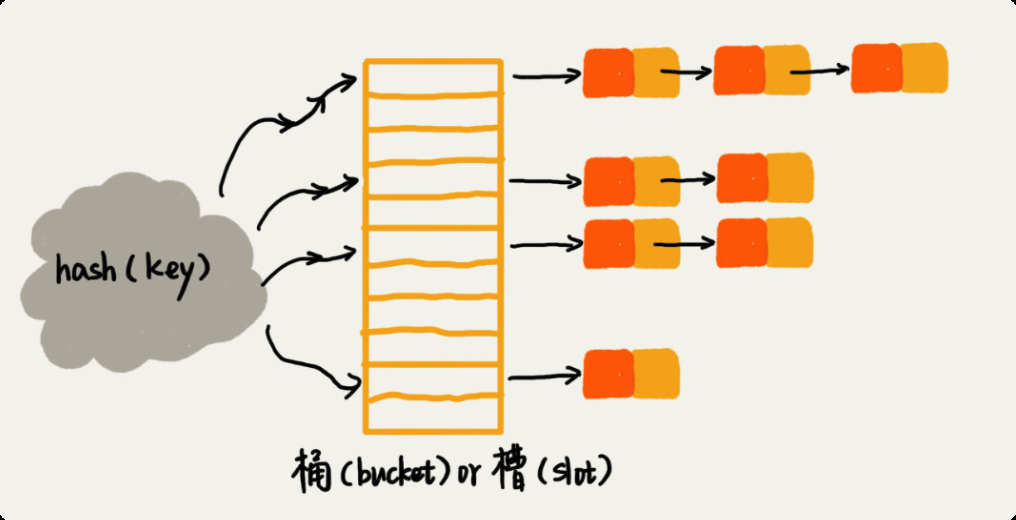
当插入的时候,我们只需要通过散列函数计算出对应的散列槽位,将其插入到对应链表中即可,所以插入的时间复杂度是 O(1)。当查找、删除一个元素时,我们同样通过散列函数计算出对应的槽,然后遍历链表查找或者删除。那查找或删除操作的时间复杂度是多少呢?实际上,这两个操作的时间复杂度跟链表的长度 k 成正比,也就是 O(k)。对于散列比较均匀的散列函数来说,理论上讲,k=n/m,其中 n 表示散列中数据的个数,m 表示散列表中“槽”的个数,那么n/m 就是 每个链表的结点的个数。
3. 如何选择冲突解决方法?
开放寻址法和链表法。这两种冲突解决办法在实际的软件开发中都非常常用。比如,Java 中 LinkedHashMap 就采用了链表法解决冲突,ThreadLocalMap 是通过线性探测的开放寻址法来解决冲突。
这两种冲突解决方法各有什么优势和劣势,又各自适用哪些场景?
1. 开放寻址法
我们先来看看,开放寻址法的优点有哪些。开放寻址法不像链表法,需要拉很多链表。散列表中的数据都存储在数组中,可以有效地利用 CPU 缓存加快查询速度。而且,这种方法实现的散列表,序列化起来比较简单。链表法包含指针,序列化起来就没那么容易。你可不要小看序列化,很多场合都会用到的。
我们再来看下,开放寻址法有哪些缺点。用开放寻址法解决冲突的散列表,删除数据的时候比较麻烦,需要特殊标记已经删除掉的数据。而且,在开放寻址法中,所有的数据都存储在一个数组中,比起链表法来说,冲突的代价更高。所以,使用开放寻址法解决冲突的散列表,装载因子的上限不能太大。这也导致这种方法比链表法更浪费内存空间。所以,当数据量比较小、装载因子小的时候,适合采用开放寻址法。这也是 Java 中的ThreadLocalMap使用开放寻址法解决散列冲突的原因。
2. 链表法
首先,链表法对内存的利用率比开放寻址法要高。因为链表结点可以在需要的时候再创建,并不需要像开放寻址法那样事先申请好。实际上,这一点也是我们前面讲过的链表优于数组的地方。链表法比起开放寻址法,对大装载因子的容忍度更高。开放寻址法只能适用装载因子小于 1 的情况。接近 1 时,就可能会有大量的散列冲突,导致大量的探测、再散列等,性能会下降很多。但是对于链表法来说,只要散列函数的值随机均匀,即便装载因子变成 10,也就是链表的长度变长了而已,虽然查找效率有所下降,但是比起顺序查找还是快很多。
链表因为要存储指针,所以对于比较小的对象的存储,是比较消耗内存的,还有可能会让内存的消耗翻倍。而且,因为链表中的结点是零散分布在内存中的,不是连续的,所以对 CPU 缓存是不友好的,这方面对于执行效率也有一定的影响。当然,如果我们存储的是大对象,也就是说要存储的对象的大小远远大于一个指针的大小(4 个字节或者 8 个字节),那链表中指针的内存消耗在大对象面前就可以忽略了。
实际上,我们对链表法稍加改造,可以实现一个更加高效的散列表。那就是,我们将链表法中的链表改造为其他高效的动态数据结构,比如跳表、红黑树。这样,即便出现散列冲突,极端情况下,所有的数据都散列到同一个桶内,那最终退化成的散列表的查找时间也只不过是 O(logn)。这样也就有效避免了前面讲到的散列碰撞攻击。
装载因子
用装载因子(load factor)来表示hash表中空位的多少。
装载因子的计算公式是:散列表的装载因子=填入表中的元素个数/散列表的长度
装载因子越大,说明空闲位置越少,冲突越多,散列表的性能会下降。
对于动态散列表来说,数据集合是频繁变动的,我们事先无法预估将要加入的数据个数,所以我们也无法事先申请一个足够大的散列表。随着数据慢慢加入,装载因子就会慢慢变大。当装载因子大到一定程度之后,散列冲突就会变得不可接受。这个时候,我们该如何处理呢?
针对散列表,当装载因子过大时,我们也可以进行动态扩容,重新申请一个更大的散列表,将数据搬移到这个新散列表中。假设每次扩容我们都申请一个原来散列表大小两倍的空间。如果原来散列表的装载因子是 0.8,那经过扩容之后,新散列表的装载因子就下降为原来的一半,变成了 0.4。
如何实现这样一个散列表
三个方面来考虑设计思路:
设计一个合适的散列函数;
定义装载因子阈值,并且设计动态扩容策略;
选择合适的散列冲突解决方法。