栈和队列
leetcode84. 柱状图的最大矩形
2021-05-17 341 4
简介 力扣的第84题,柱状图的最大矩形,连接 https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
解题思路
看到这个题,如果没有任何提示,如何想到用“栈” 来解决的? 下面来进行一步步分析。
先不考虑太多,上来就暴力求解下。(很多时候,优化方案是在通过暴力手段解决问题后,得到了新的思路,进而优化,得到了更好的解决方案,暴力解决算法问题,并不丢人!!!)
1. 暴力求解法1
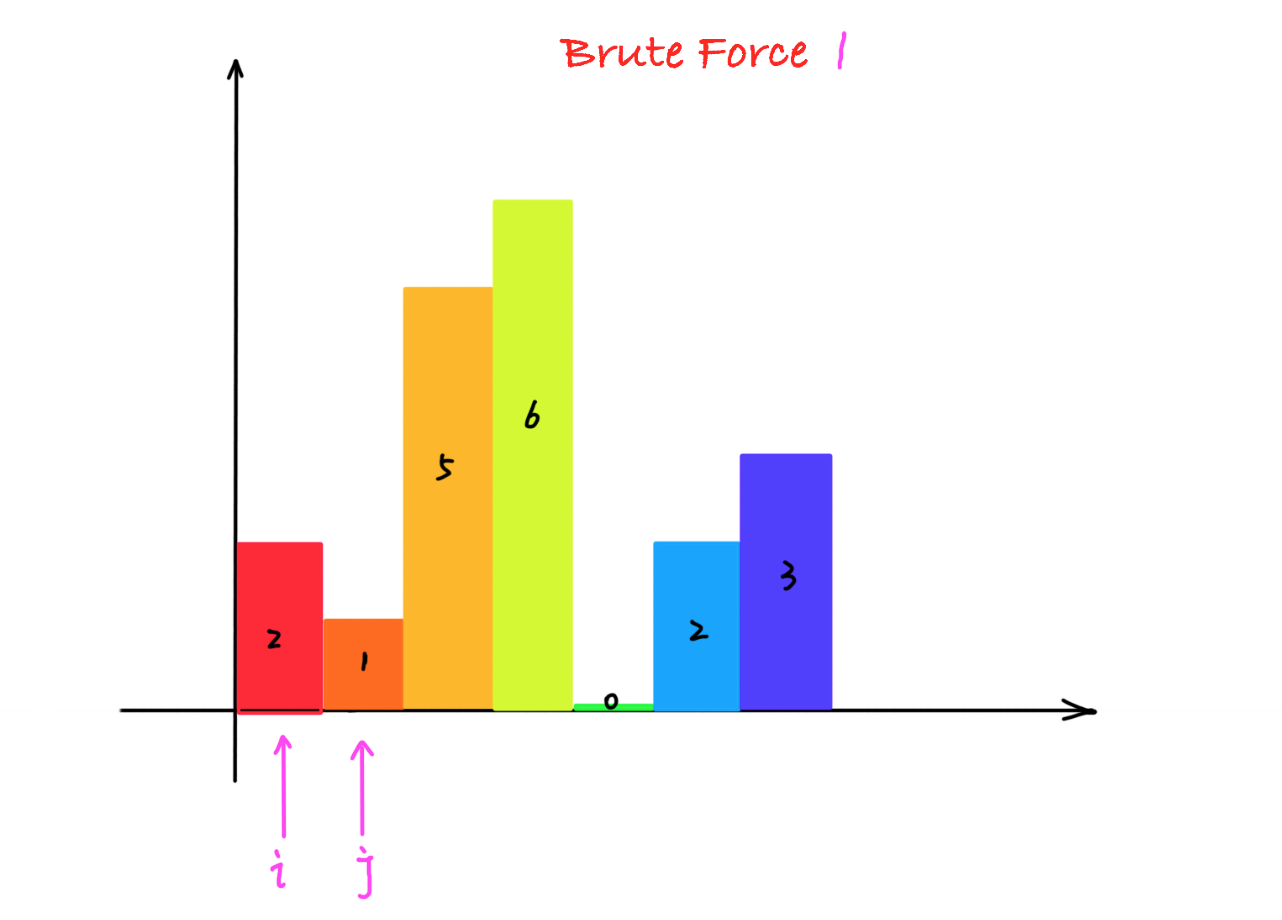
两层循环, 依次向后遍历, 一边遍历一边记录最小的“高度”,计算面积, 记录最大面积
遍历结束后, 所有的单个柱子的面积以及组合柱子的面积全部计算了一次,那最大面积也就得到了,算法的时间复杂度是 O(n^2)、
以C++代码为例:
class Solution {public: int largestRectangleArea(vector<int>& heights) { int length = heights.size(); int minHeight; int maxArea = 0; int width = 1; for(int i = 0; i < length; ++i) { // 单个柱子的面积 maxArea = maxArea > heights[i] * 1 ? maxArea : heights[i] * 1;
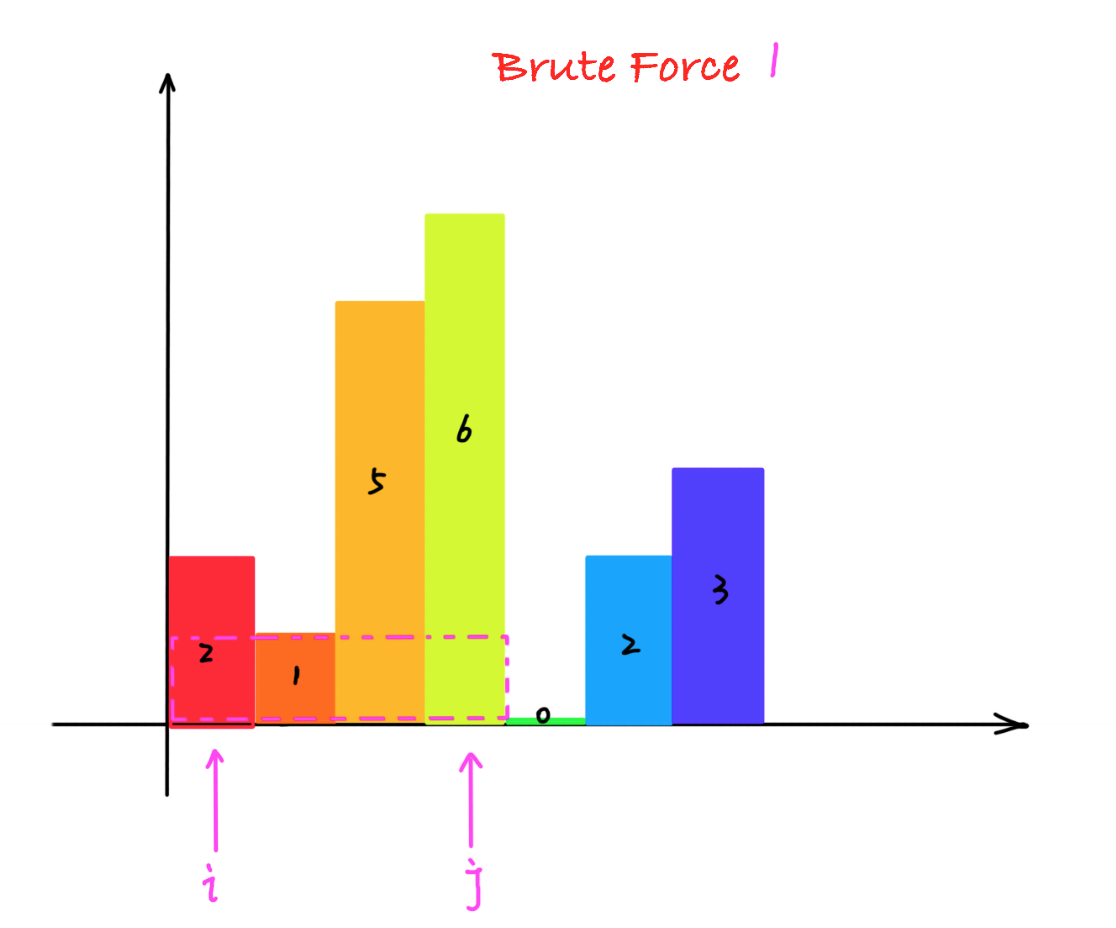
// 重置 高和宽 minHeight = heights[i]; width = 1;
// 组合柱子的面积 for(int j = i + 1; j < length; ++j) { minHeight = minHeight < heights[j] ? minHeight : heights[j]; ++width; maxArea = maxArea > minHeight * width ? maxArea : minHeight * width; } } return maxArea; }};2. 暴力求解法2
很明显,暴力解法1存在大量的重复计算和没必要的计算, 因为内层循环的第一次遍历结束后,所有的柱子都遍历一次了, 也就是计算机知道了每个柱子的高度。
那么计算最大面积时,可以跳过一些情况,不进行计算。
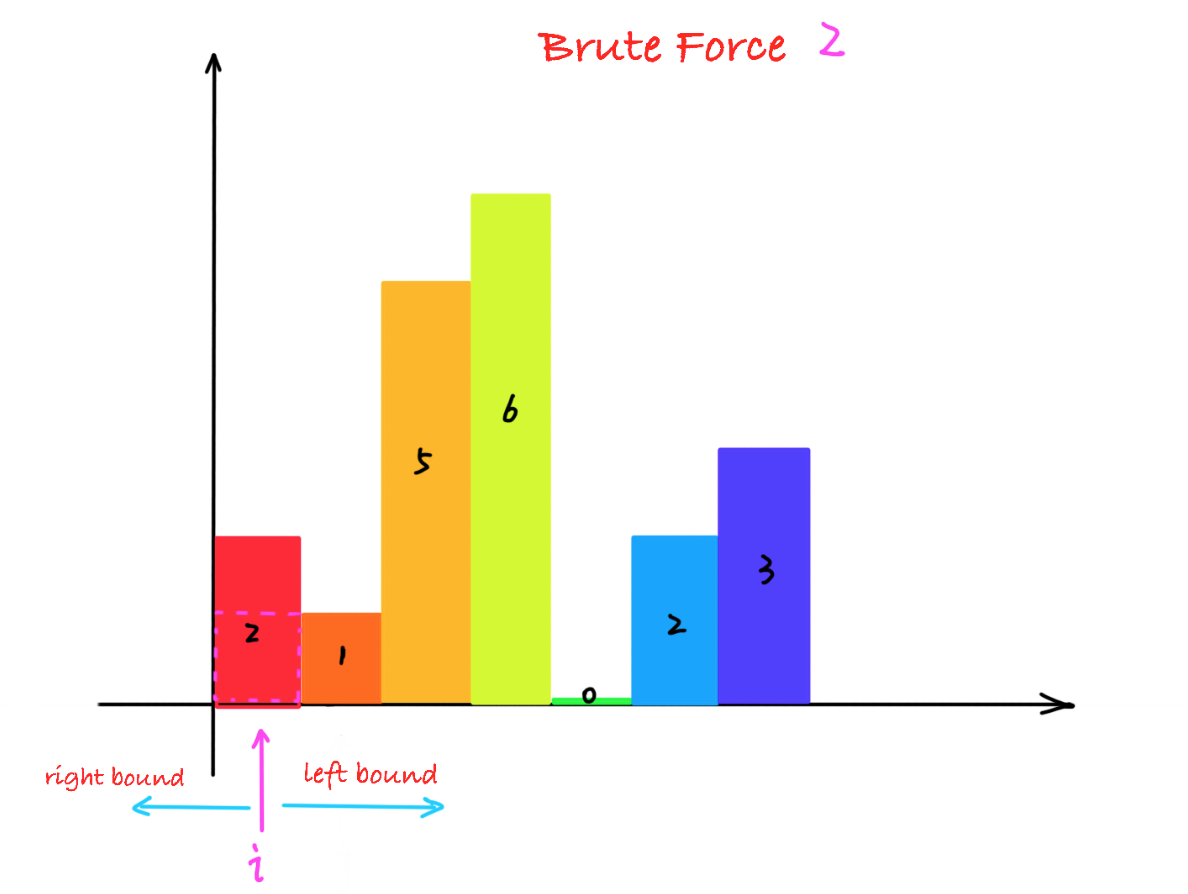
我们可以枚举每一个柱子, 寻找它的左右边界, 计算面积并记录最大面积,那么不是柱子的左右边界的地方,并没有计算面积,虽然算法的时间复杂度还是O(n^2),但相比于暴力求解法1,减少了大量的计算,这个优化方案合理可行。
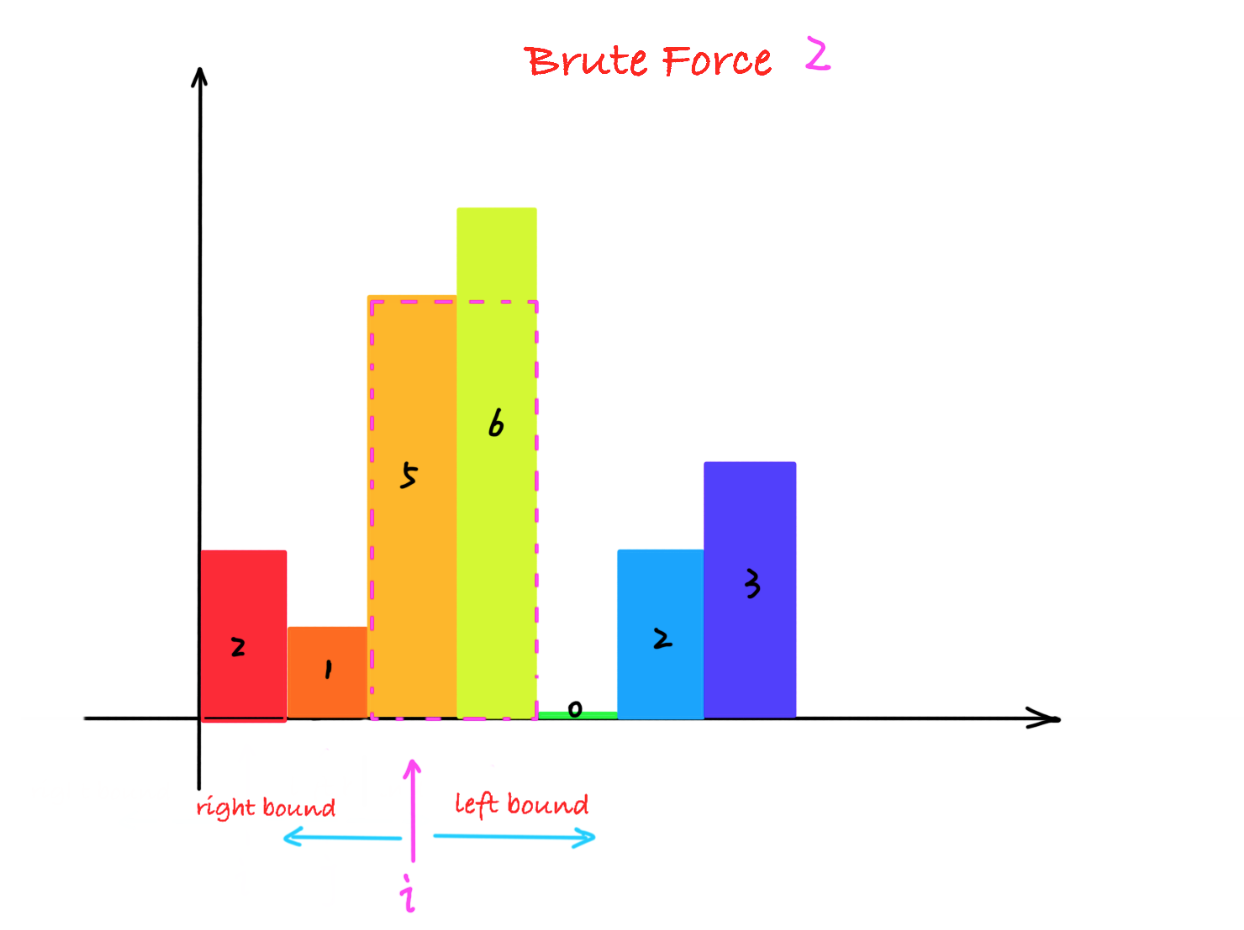
以Java代码为例
class Solution { public int largestRectangleArea(int[] heights) { int len = heights.length; int maxarea = 0;
// 枚举每个柱子 for(int i = 0; i < len; i++) { // 寻找左边界 int left = 0; for(left = i - 1; left >= 0; left--) { if(heights[left] < heights[i]) break; }
int right = 0; // 寻找右边界 for(right = i + 1; right < len; right++) { if(heights[right] < heights[i]) break; }
// 计算最大面积 maxarea = Math.max(maxarea, heights[i] * (right - left - 1)); } return maxarea; }}3. 最终优化方案----递增栈
对于暴力求解法2,我们发现对于左右边界的查找是有规律的
1.如果柱子的高度递减,那么每个柱子的左边界就是第一根柱子,右边界就是本身。
2.如果柱子的高度递增,那么每个柱子的右边界就是最后一根柱子,左边界就是本身。
有了这样的思路,那么对于无序的柱子组合,我们可以将其拆分, 保证每一个局部是有序的,然后计算最大面积就容易了。
局部的柱子有序后,那如何保存这些局部的柱子呢? 我们发现这些柱子,具有最近相关性,所以使用栈保存这些有序的柱子。
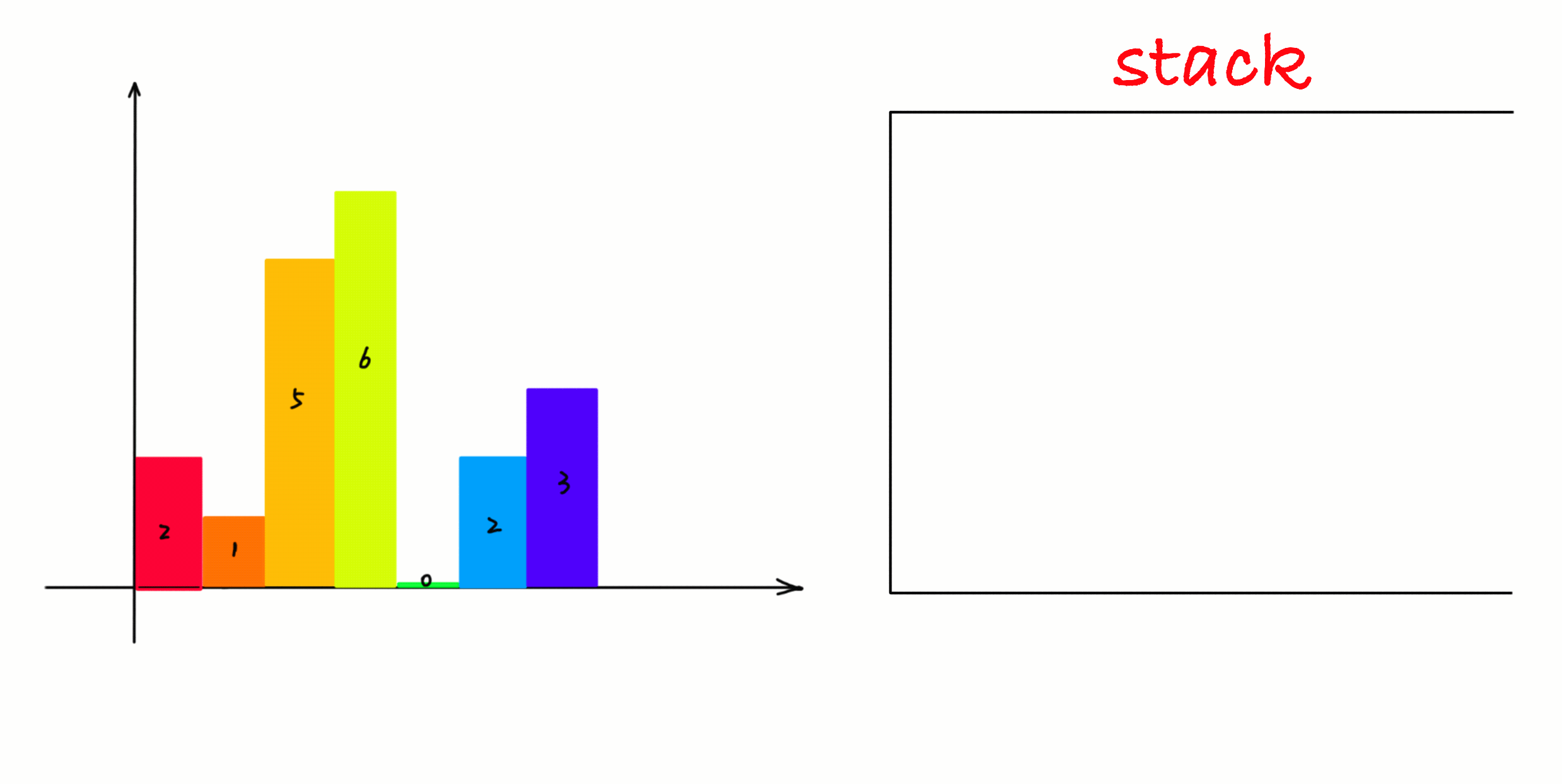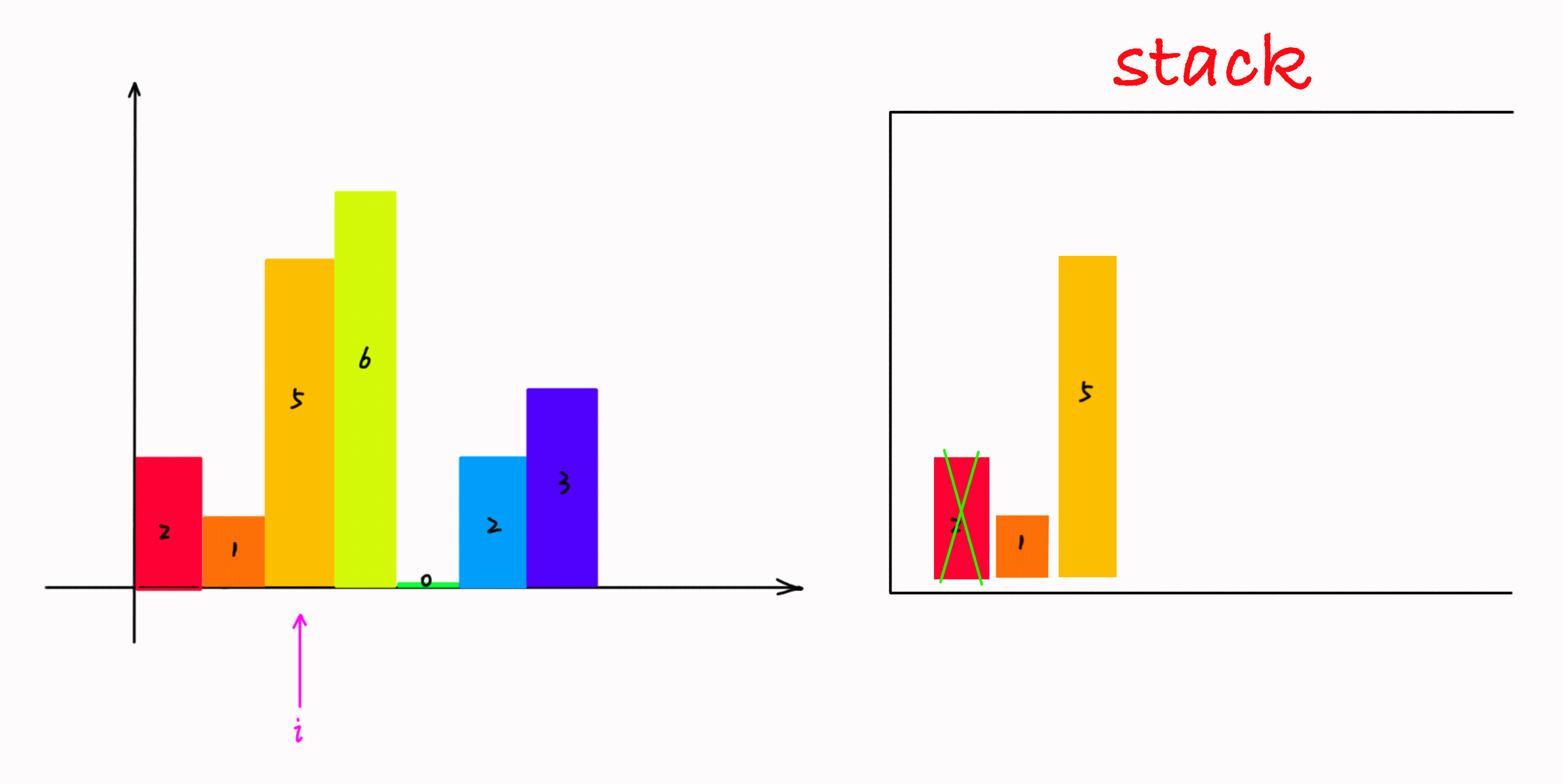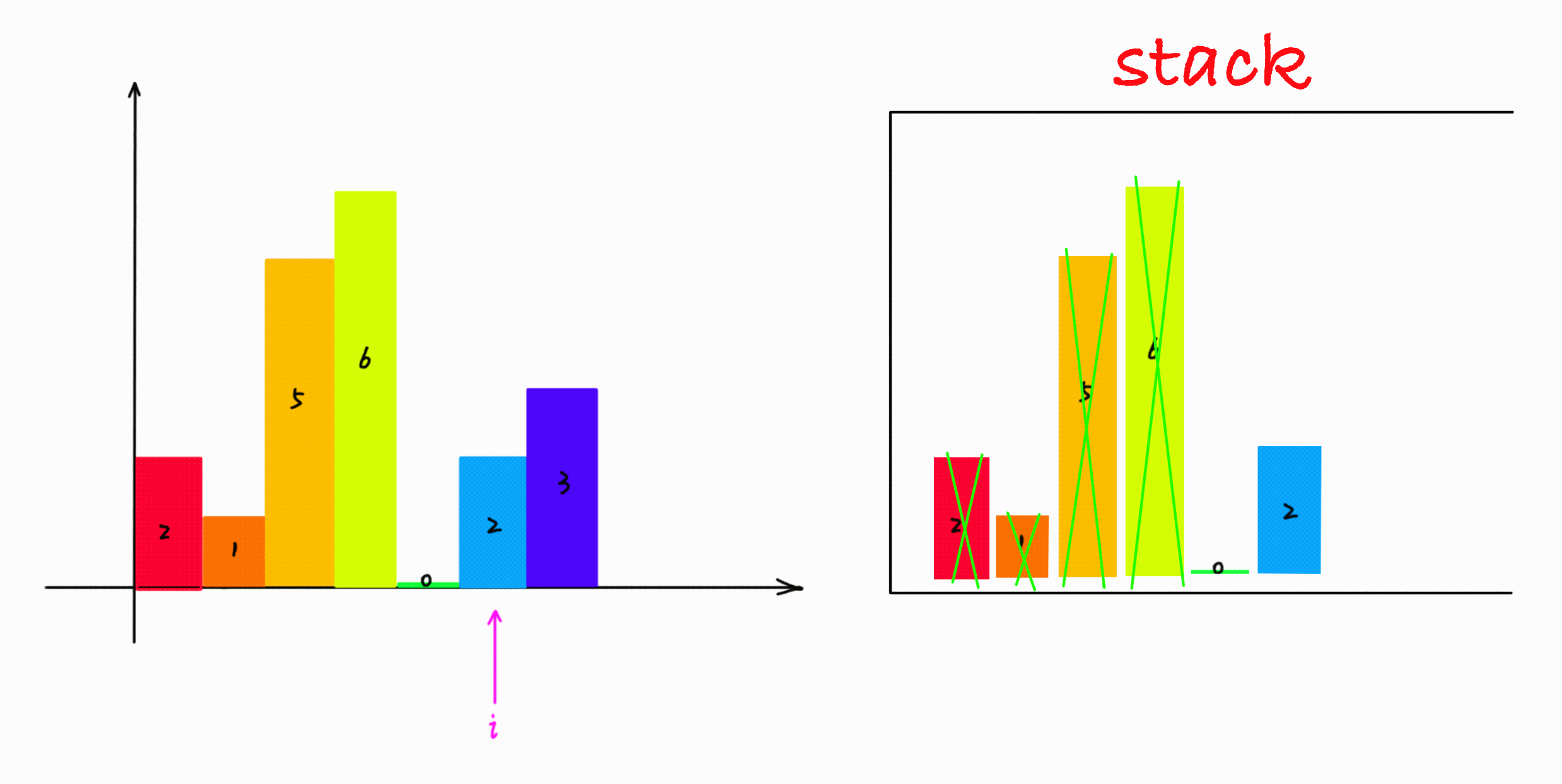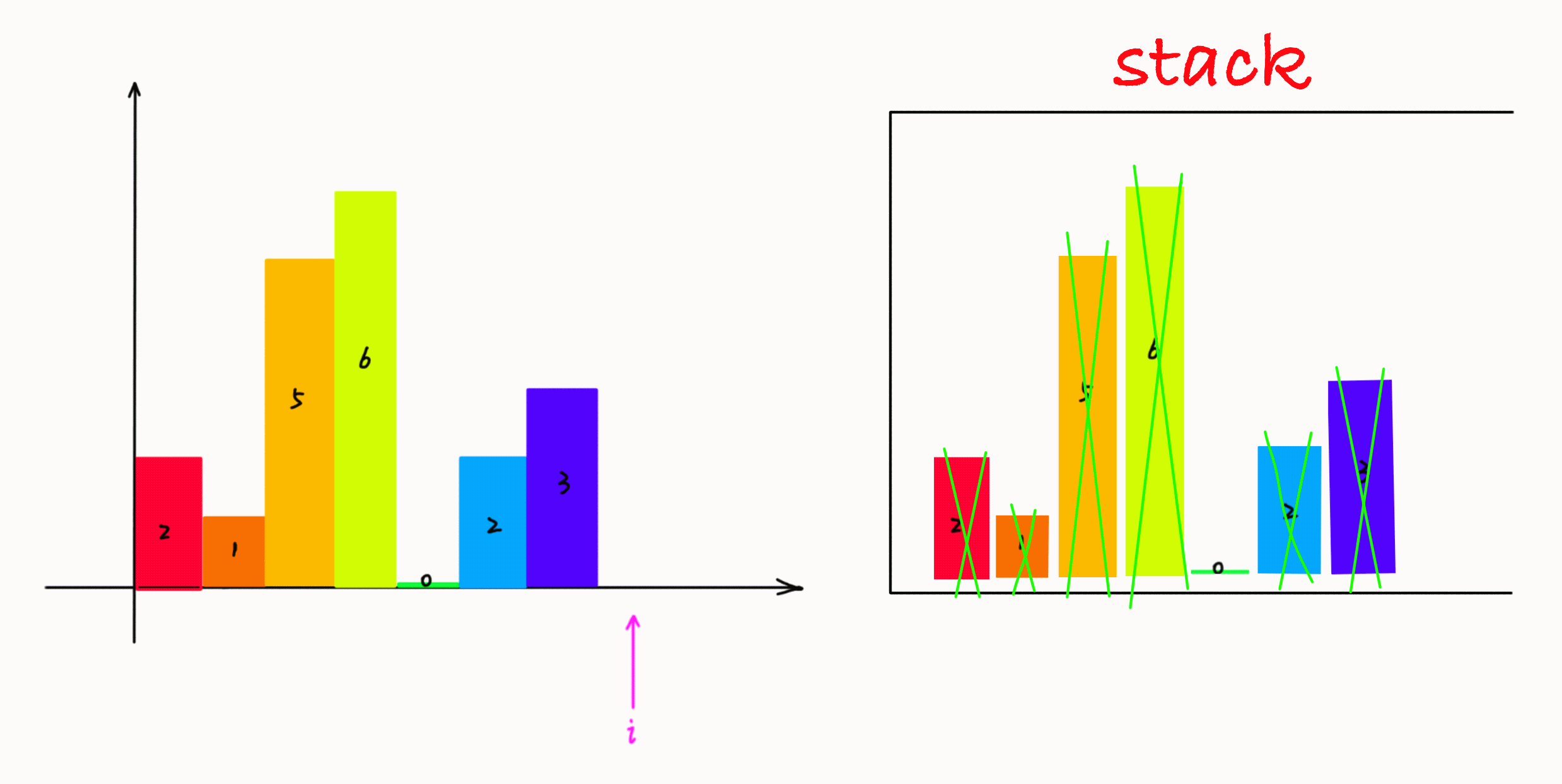
1. 遍历每一个柱子,如果当前遍历的柱子比栈顶大,那么当前柱子入栈,说明还没有找到右边界。
2. 如果当前遍历的柱子比栈顶小,那么栈顶的柱子找到了右边界,当前遍历柱子的左边界就是栈中栈顶元素的下一个元素的位置,这时候面积就可以计算了。
简单说来就是: 大则入栈,小则处理栈中元素计算最大面积,直到栈中没有比当前遍历的柱子更短的柱子,然后将当前遍历的柱子再入栈。
遍历结束后, 栈中可能有数据, 这时候的数据必然是递增的, 同时没根柱子的右边界是柱状图的最后一根柱子,每个柱子的左边界就是他本身,那么面积就可以很容易计算了。
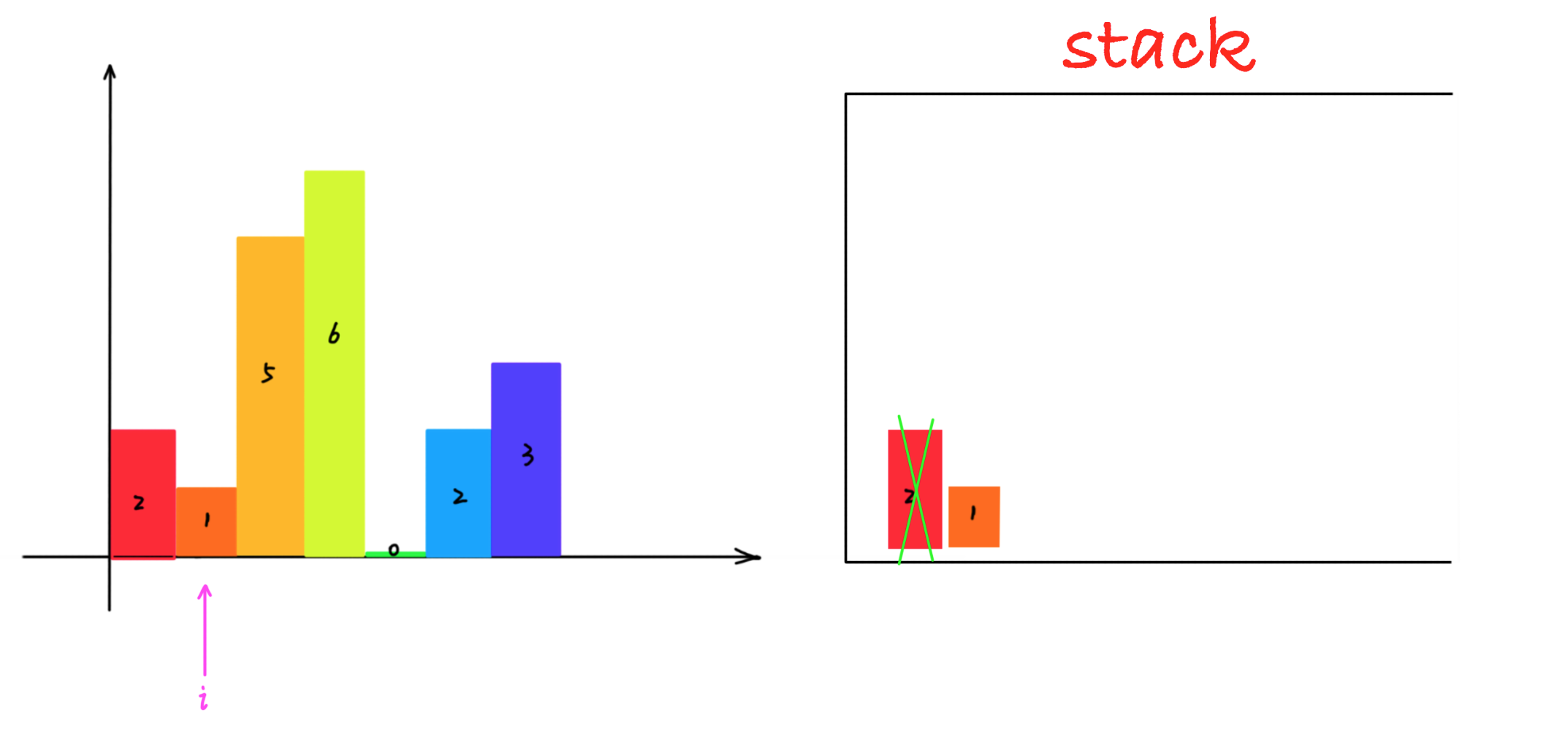
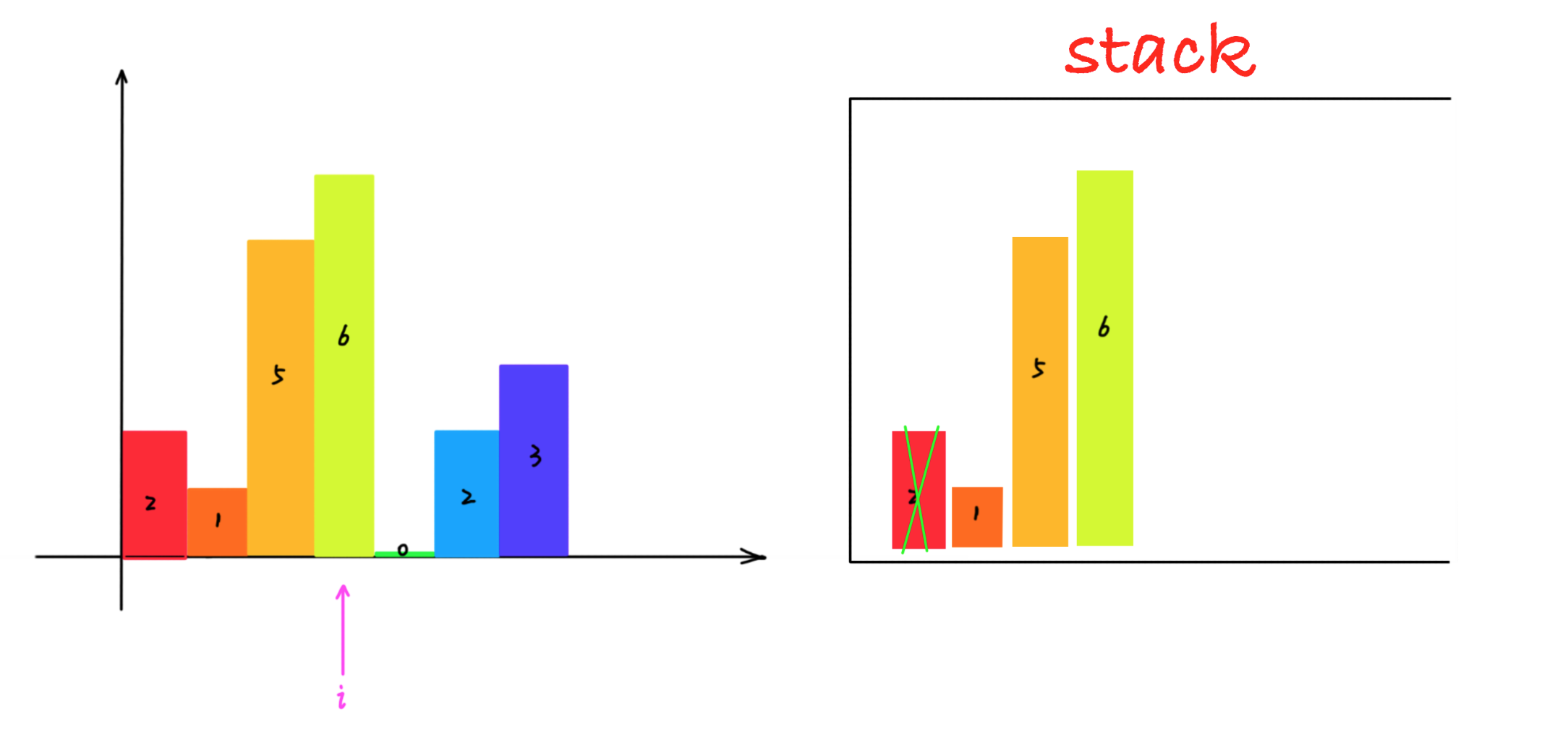
动画如下所示:
视频(可暂停观看)
// C++class Solution {public: int largestRectangleArea(vector<int>& heights) { int len = heights.size(); int maxarea = 0; stack<int> stk;
for(int i = 0; i < len; ++i) { // 只要栈不为空,并且当前遍历的数据小于栈顶元素,则说明找到了右边界 while(!stk.empty() && heights[i] < heights[stk.top()]) { // 右边界 heights[i] int h = heights[stk.top()]; stk.pop(); // 出栈后,如果栈为空,说明出栈的柱子目前遍历的最短的柱子,否则计算宽度差 int w = stk.empty() ? i : i - stk.top() - 1; maxarea = max(h * w, maxarea); }
// 栈为空或者当前遍历的数据大于等于栈顶数据,则入栈,不会执行上面的while循环 // 保证了栈中的数据总是递增的 比如 0 1 2 2 3 4 4 5 6 ... stk.push(i); }
// 处理剩余栈中的数据(递增的数据,右边界是柱状图中最右边的柱子) while(!stk.empty()) { int h = heights[stk.top()]; stk.pop();
// 出栈后,如果栈为空,说明出栈的柱子目前遍历的最短的柱子,否则计算宽度差 int w = stk.empty() ? len : len - stk.top() - 1; maxarea = max(h * w, maxarea); }}// Javaclass Solution { public int largestRectangleArea(int[] heights) { int len = heights.length; int maxarea = 0; Stack<Integer> stk = new Stack<Integer>();
for(int i = 0; i < len; ++i) {
// 只要栈不为空,并且当前遍历的数据小于栈顶元素,则说明找到了右边界 while(!stk.empty() && heights[i] < heights[stk.peek()]) { // 右边界 heights[i] int h = heights[stk.peek()]; stk.pop(); // 出栈后,如果栈为空,说明出栈的柱子目前遍历的最短的柱子,否则计算宽度差 int w = stk.empty() ? i : i - stk.peek() - 1; maxarea = Math.max(h * w, maxarea); }
// 栈为空或者当前遍历的数据大于等于栈顶数据,则入栈,不会执行上面的while循环 // 保证了栈中的数据总是递增的 比如 0 1 2 2 3 4 4 5 6 ... stk.push(i); }
// 处理剩余栈中的数据(递增的数据,右边界是柱状图中最右边的柱子) while(!stk.empty()) { int h = heights[stk.peek()]; stk.pop();
// 出栈后,如果栈为空,说明出栈的柱子目前遍历的最短的柱子,否则计算宽度差 int w = stk.empty() ? len : len - stk.peek() - 1; maxarea = Math.max(h * w, maxarea); } return maxarea; }}##Pythonclass Solution: def largestRectangleArea(self, heights: List[int]) -> int: maxarea = 0 stk = list() for i in range(len(heights)): # 只要栈不为空,并且当前遍历的数据小于栈顶元素,则说明找到了右边界 while stk and heights[i] < heights[stk[-1]]: h = heights[stk[-1]]; stk.pop()
# 出栈后,如果栈为空,说明出栈的柱子目前遍历的最短的柱子,否则计算宽度差 w = i - stk[-1] - 1 if stk else i maxarea = max(h * w, maxarea)
# 栈为空或者当前遍历的数据大于等于栈顶数据,则入栈,不会执行上面的while循环 # 保证了栈中的数据总是递增的 比如 0 1 2 2 3 4 4 5 6 ... stk.append(i) # 处理剩余栈中的数据(递增的数据,右边界是柱状图中最右边的柱子) while stk: h = heights[stk[-1]] stk.pop()
# 出栈后,如果栈为空,说明出栈的柱子目前遍历的最短的柱子,否则计算宽度差 w = len(heights) - stk[-1] - 1 if stk else len(heights) maxarea = max(h * w, maxarea) return maxarea